トップページへ

パソコンでフラクタルを描画してみようと思い立ちました。
1980年代の中頃、N88-BASIC言語で書かれたマンデルブロー集合の描画プログラムをパソコン雑誌で見つけ、 当時使っていたPC-8800（NEC製）にこのプログラムを打ち込んで描画し、その不可思議な形状を楽しんだものです。
最近の言語で記述されている関連情報を検索したところ、石立喬さんが2006年に公開している、以下の2つの情報を見つけました。
　　「マンデルブロー集合による新しいフラクタル図形を探索する」
　　「ジュリア集合の色付けを工夫して芸術的なフラクタル図形を描く」
これらの描画プログラムはjava言語で書かれていましたが、これを作者が常用しているC#言語に置き換えて描画し、また動画にして、フラクタルの世界で遊んでみました。

漸化式　Z_n+1 = Z_n² + A + Bｉ で定義される複素数の数列｛Zn｝において、 Zの初期値を0 + 0ｉ とした場合に、この複素数列が発散しないような実数部Aと虚数部Bの組み合わせの集合をマンデルブロー集合といいます。
パソコンでマンデルブロー集合を描画する場合、実数部Aを横軸に、虚数部Bを縦軸にとってプロットします。
また発散しない領域を黒色で描画し、発散する領域については発散したとみなす閾値をこえた時点の繰り返し回数 ｎ の値に応じて色分けをすると、 カラー化されたマンデルブロー集合のパターンが得られます。
下図は、発散領域を16諧調に色分けして作成したマンデルブロー集合の図です。

　　　

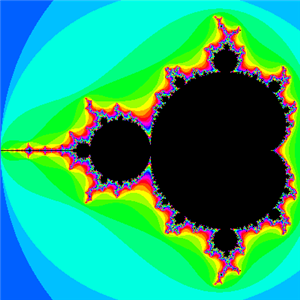
マンデルブロー集合の細部構造は多岐にわたり変化に富んでいるので、新たな構造を見つけてみようという誘惑にかられます。
パソコンでマンデルブロー集合の綺麗な画像を得るためには描画時の計算精度をあげる必要がありますが、
計算精度をあげるほどパソコンの処理に時間がかかるため、適当なところで妥協をすることになります。

作者の手持ちパソコンでマンデルブロー集合の動画を作成し、YouTube に投稿しました。
　　マンデルブロ集合�@ − オーロラの世界
　　マンデルブロ集合�A − フラクタルフローラ
　　マンデルブロ集合�B − 虹色らせんの世界
　　マンデルブロ集合�C − アラベスクの世界
　　マンデルブロ集合�D − 花火の世界
視聴していただければ幸いです。

また、それらの動画に関連した画像を画像ギャラリーのページ にあげておきましたので、参照してください。

漸化式　Z_n+1 = Z_n² + A + Bｉ で定義される複素数の数列｛Zn｝において、実数部 Aと虚数部 B を指定して、 この複素数列が発散しないような Z = X + Yｉ の初期値 X₀、Y₀ の集合をジュリア集合（正式には充填ジュリア集合）といいます。
従って、指定された A、Bの値に応じて、異なったジュリア集合が存在します。
パソコンでジュリア集合を描画する場合、初期値の実数部 X₀ を横軸に、初期値の虚数部 Y₀ を縦軸にとってプロットします。
また、マンデルブロー集合の場合と同様に、発散領域をカラー化して描画しました。

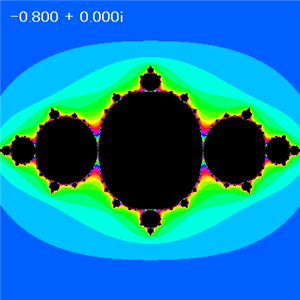
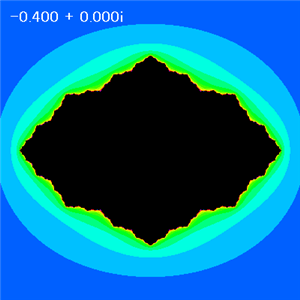
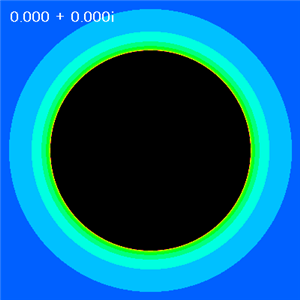
A = -0.8	A = -0.4	A = 0
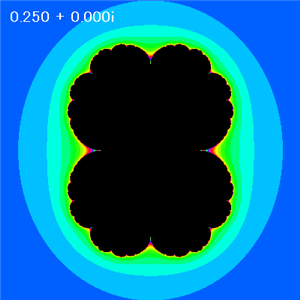
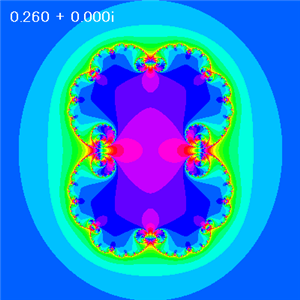
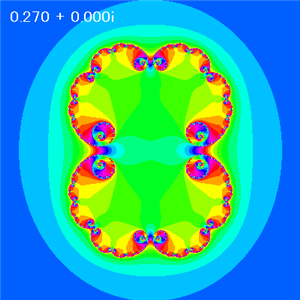
A = 0.25	A = 0.26	A = 0.27
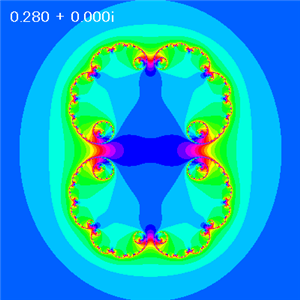
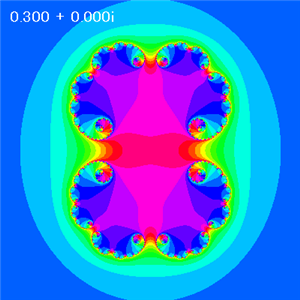
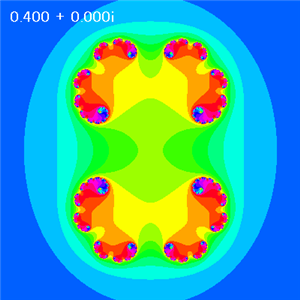
A = 0.28	A = 0.30	A = 0.40

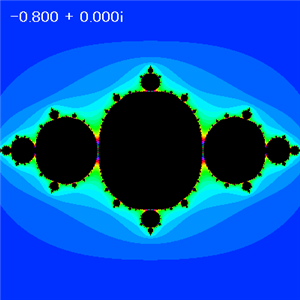
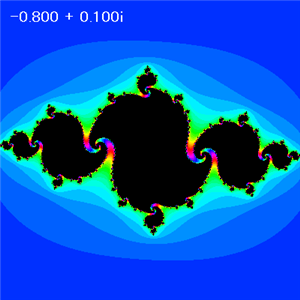
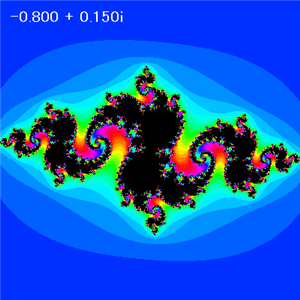
B = 0	B = 0.1	B = 0.15
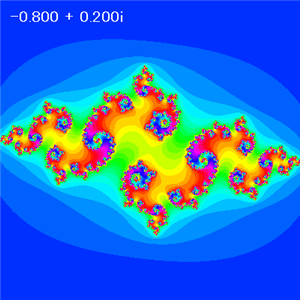
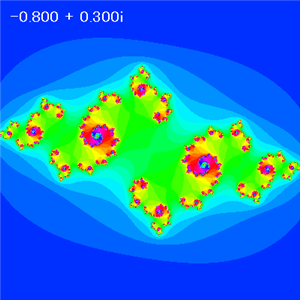
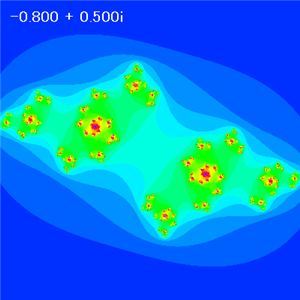
B = 0.2	B = 0.3	B = 0.5

ご質問、ご意見、ご感想、バグ等のご連絡は、 こちらへ

トップページへ